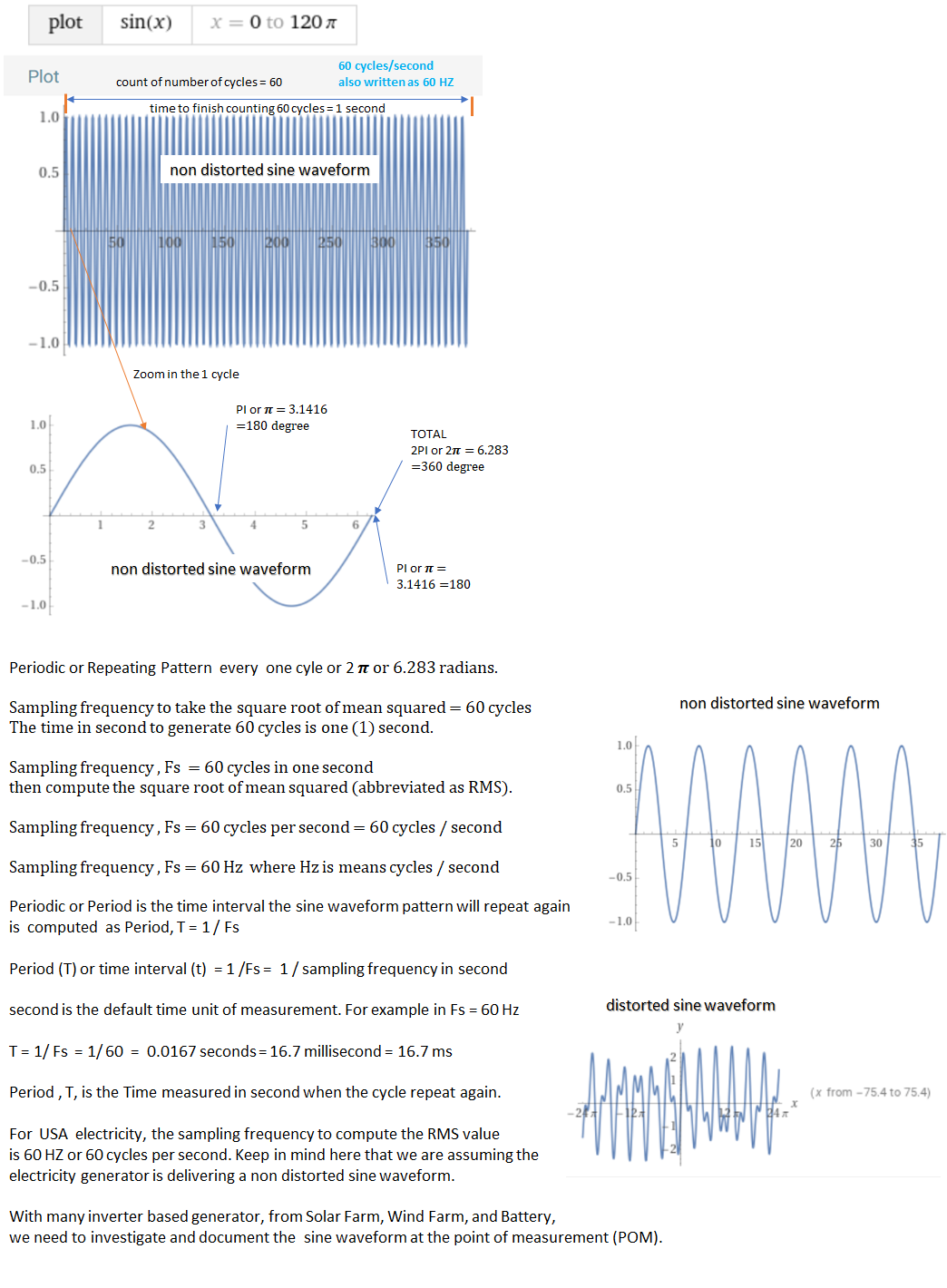
Freq: 1 Phase: 0 Click the animation button to start
.
.
.
Injecting 3rd harmonics to fundamental at 180 HzFreq: 2 Phase: 0
.
.
.
Injecting 5th harmonics to fundamental at 300 HzFreq: 3 Phase: 0
.
.
.
Addition of Waves 1, 2, and 3

















Credit to: Geogebra - A B Cron for sharing publicly: Adding sine and cosine function graphically
3rd harmonic frequency injected to fundamental frequency
Created by Apolinario "Sam" Ortega using
Geogebra 7/9/2016
Credit to: Geogebra - Malin Christersson for sharing publicly: superposition of waves
Modified by Apolinario "Sam" Ortega for inductive circuit voltage, current, and power profile. Date created 7/9/2016
Shown above is the decomposition of distorted or noisy waveform. It is made up of fundamental waveform, (f1) 3rd harmonics (f2) and 5th harmonics (f3), and DC component (f4)
French mathematician Jean Baptiste Fourier demonstrated that any distorted periodic sine waveform can be decomposed into several fundamental sine wave.
To illustrate his discovery, look at the white color distorted periodic sine wave shown below. What Fourier discovered is he can recreate the distorted periodic sine wave by simply adding three perfect sine waveforms but at different cycle. For example if you add the 1 cycle sine wave + 3 cycle sine wave + 5 cycle sine wave the resulting wave form is the distorted sine wave form white color .
Why this knowledge is very important? This knowledge is very important because of the growing power electronics in solar farms and wind farms. The power electronics are known
to distort the perfect sine wave. With frequency spectrum analyzer we can see the dominant harmonic content that was added to the perfect sine wave. For example,
if we discovered from analyzing frequency spectrum that 3rd harmonics (meaning for US electric grid, 60 Hz is the electric frequency value,
3rd harmonics is 60 hz times 3 = 180 Hz) is causing the distortion of perfect sine voltage waveform or perfect current waveform then before we connect
to electric grid the inverter based power electronics we can install a filter that removes the 3rd harmonics generated by power electronics. Disclaimer:
Please note this example was used for illustration only.
Freq: 1 Phase: 0 Click the animation button to start
.
.
.
Injecting 3rd harmonics to fundamental at 180 HzFreq: 2 Phase: 0
.
.
.
Injecting 5th harmonics to fundamental at 300 HzFreq: 3 Phase: 0
.
.
.
Addition of Waves 1, 2, and 3 Creating complex waveforms can be made by adding three series of sine waves with different frequencies. Use the above button to Increase
or decrease the frequencies and increment the phase of the component sine waves to see how they add together.

Fourier analysis is a mathematical tool you use to show how many series of sine waves frequencies you need to add to create a complex distored sine waveform. As you can see from above waveform the total of seven series of sine waves with different frequencies generated a new complex distorted sine waveform that looks like a square waveform. The process of adding together series of sine waves with different frequencies are called Fourier synthesis. . Transformation of sine wave in time domain to frequency domain can be done using fast Fourier transform or fft.
Shown below is an illustration of fft using Matlab software.

As we progress in 4th industrial revolution, waveform analysis knowledge and understanding is very important. Shown below is an example of waveform analysis use in system protection relay and synchrophasor phasor measurement units for electrical system network situational awareness.
Review of Sampling Frequency
 Fundamental (60Hz) + 3rd (1 peak) + 5th (1 peak) + 7th (1 peak) Harmonic Addition
Fundamental (60Hz) + 3rd (1 peak) + 5th (1 peak) + 7th (1 peak) Harmonic Addition















Electro Magnetic Transient Program Simulation Waveform (EMTP) shared in LinkedIn by Bahram Khodabakhchian
Given the distorted waveform from EMTP study how can we do fast fourier transform (fft) to discover the dominant frequency of voltage or current?
We comply with LinkedIn Embed Term of Use
Fast Fourier Transform shared in LinkedIn by: Source Credit to:
Bingsen Wang, PhD
Global Manager, HV Safety Integration at Stellantis, SMIEEE
We comply with LinkedIn Embed Term of Use
.
.
IN-V-BAT-AI is a valuable classroom tool that enhances both teaching and learning experiences. Here are some ways it can be utilized:
☑️ Personalized Learning : By storing and retrieving knowledge in the cloud, students can access tailored resources and revisit
concepts they struggle with, ensuring a more individualized learning journey.
☑️ Memory Support : The tool helps students recall information even when stress or distractions hinder their memory, making it
easier to retain and apply knowledge during homework assignments or projects.
☑️ Bridging Learning Gaps : It addresses learning loss by providing consistent access to educational materials, ensuring that
students who miss lessons can catch up effectively.
☑️ Teacher Assistance : Educators can use the tool to provide targeted interventions to support learning.
☑️ Stress Reduction : By alleviating the pressure of memorization, students can focus on understanding and applying concepts,
fostering a deeper engagement with the material.
📚 While most EdTech platforms focus on delivering content or automating classrooms, IN-V-BAT-AI solves a deeper problem: forgetting.
✨Unlike adaptive learning systems that personalize what you learn, IN-V-BAT-AI personalizes what you remember. With over 504 pieces of instantly retrievable knowledge, it's your cloud-based memory assistant—built for exam prep, lifelong learning, and stress-free recall.
"🧠 Forget less. Learn more. Remember on demand."
That's the IN-V-BAT-AI promise.
Understanding the difference between collaboration and automation

Augmented Intelligence is like a co-pilot: it accelerates problem-solving through trusted automation and decision-making, helping you recall, analyze, and decide — but it never flies solo.
Artificial Intelligence is more like an autopilot: designed to take over the controls entirely, often without asking.
IN-V-BAT-AI is a textbook example of Augmented Intelligence. It empowers learners with one-click recall, traceable results, and emotionally resonant memory tools. Our “Never Forget” promise isn't about replacing human memory — it's about enhancing it.

Note: This is not real data — it is synthetic data generated using Co-Pilot to compare and contrast IN-V-BAT-AI with leading EdTech platforms.


.
.
.
IN-V-BAT-AI just crossed 72,133 organic visits—no ads, just curiosity and word-of-mouth.
Every visit is a step toward forgetting less, recalling faster, and remembering on demand.
Never Forget. Learn on demand.
🔗 Subscribe| Year | Top 10 countries | Pages visited |
| 2023 | 1. USA 2. Great Britain 3. Germany 4. Canada 5. Iran 6. Netherlands 7. India 8. China 9. Australia 10. Philippines | 127,256 Pages / 27,541 Visitors |
| 2024 | 1. USA 2. China 3. Canada 4. Poland 5. India 6. Philippines 7. Great Britain 8. Australia 9. Indonesia 10. Russia | 164,130 Pages / 40,724 Visitors |
| Daily Site Visitor Ranking 11/14/2025 | 1. Israel 2. USA 3. China 4. Vietnam 5. Japan 6. India 7. Australia 8. Argentina 9. Brazil 10. Ukraine | Year to Date 204,611 Pages / 72,133 Visitors |