.
.
IN-V-BAT-AI solution to forgetting! No coding and no website hosting on your part.
Remember on demand is now possible!
Type here Using AI - Voice to Text Then tap SEARCH 2
Geometric Series First Term

Instruction on how to use the calculator to solve the above problem
Step 1. Enter 2 in box n2 Why? It is the second number in geometric series.
Step 2. Enter 0.3 decimal equivalent of 3/10 the recorded value for second number
Step 3. Enter 6 in box n6 Why? It is the six number in geometric series.
Step 4. Enter 1.51875 decimal equivalent of 243/160 the recorded value for the sixth number.
Then select the Solve button if needed. Usually the answer is automatic.
Step 5. The answer is letter a = the first term of geometric series
Step 6. Now you can predict the last number at any position of the geometric series. How ? Enter any integer number in box n nth to compute the expected value of the Last term, L nth term
For example n nth = 9
L nth = 5.1258
Step 7. Total number of geometric series up to the last number term or last position is calculated automatically.
How to become a millionaire in 37 days, application of geometric series
Given information you have $0.20 dollar in day 1, $0.30 in day 2, $0.45 in day 3, $0.675 in day 4. Your business is growing and your income grows geometrically or exponentially at constant rate of 1.5 from previous day. What will be your money in day 12, in day 24, in day 48 and in day 50?
As you can see it is possible to become a millionaire in 37 days.
The hardest part is finding and sustaining a business that grows exponentially at a rate of 1.5 per day.
Here is my work in progress demonstration on how to achieve $1 million dollar in 37 days. I am still solving the hardest part finding a solution to old problem that students or teachers or parents willing to
pay for my online service.
My idea is to solve the learning loss or forgetting problem of every student by offering $1.70 per month online subscription to never forget subscription for reviewer, formula, and calculator.
Creating the demand or need for my service is the hardest part because if nobody is
willing to pay for the online subscription service that I am offering then there no is geometric series at a constant rate of 1.5 per day. The next challenge is to cover the overhead expenses to automate the online registration, online payment, online content delivery, and online subscription renewal or cancellation.
I believe using geometric series principle it is possible for me to become a millionaire in 37 days even if my company is a one man online subscription company.
| Days | Savings Money | Accumulated Savings | Subscription $1.70 per Month Qty Sold Per Day | Total $ Subscription | Accumulated $ Sales |
|---|---|---|---|---|---|
| Day 1 | $0.20 | - | - | - | - |
| Day 2 | $0.30 | $0.50 | - | - | - |
| Day 3 | $0.45 | $0.95 | - | - | - |
| Day 4 | $0.68 | $1.63 | 1 | $1.70 | $1.70 |
| Day 5 | $1.01 | $2.64 | 1 | $1.70 | $3.40 |
| Day 6 | $1.52 | $4.16 | 1 | $1.70 | $5.10 |
| Day 7 | $2.28 | $6.44 | 1 | $1.70 | $6.80 |
| Day 8 | $3.42 | $9.86 | 1 | $1.70 | $8.50 |
| Day 9 | $5.13 | $14.99 | 3 | $5.10 | $13.60 |
| Day 10 | $7.69 | $22.68 | 6 | $10.20 | $23.80 |
| Day 11 | $11.53 | $34.21 | 6 | $10.20 | $34.00 |
| Day 12 | $17.30 | $51.50 | 10 must be sold by automation | $17.00 | $51.00 |
| Day 13 | $25.95 | $77.46 | 15 must be sold by automation | $25.50 | $76.50 |
| Day 14 | $38.92 | $116.38 | 22 must be sold by automation | $37.40 | $113.90 |
| Day 15 | $58.39 | $174.77 | 36 must be sold by automation | $61.20 | $174.10 |
| I will | get | the savings | $87.58 | from subscription | |
| Day 16 | $87.58 | $262.35 | 52 must be sold by automation | $88.40 | $262.50 |
| I will | get | the savings | $131.37 | from subscription | |
| Day 17 | $131.37 | $393.72 | 78 must be sold by automation | $132.60 | $395.10 |
| I will | get | the savings | $197.05 | from subscription | |
| Day 18 | $197.05 | $590.77 | 115 must be sold by automation | $195.50 | $590.60 |
| I will | get | the savings | $295.59 | from subscription | |
| Day 19 | $295.59 | $886.36 | 174 must be sold by automation | $295.80 | $886.40 |
| I will | get | the savings | $443.70 | from subscription | |
| Day 20 | $443.37 | $1,329.73 | 261 must be sold by automation | $443.70 | $1,330.10 |
| Day 21 | $665.05 | $1,994.78 | 391 must be sold by automation | $664.70 | $1,994.80 |
| Day 22 | $997.58 | $2,992.33 | 587 must be sold by automation | $997.90 | $2,992.70 |
| Day 23 | $1,496.37 | $4,488.70 | 880 must be sold by automation | $1,496 | $4,488.70 |
| Day 24 | $2,244.55 | $6,733.24 | 1,320 must be sold by automation | $2,244 | $6,732.70 |
| Day 25 | $3,366.82 | $10,100.07 | 1,981 must be sold by automation | $3,367.7 | $10,100.40 |
| Day 26 | $5,050.23 | $15,150.30 | 2,971 must be sold by automation | $5,050.70 | $15,151.10 |
| Day 27 | $7,575.35 | $22,725.65 | 4,456 must be sold by automation | $7,575.20 | $22,726.30 |
| Day 28 | $11,363.03 | $34,088.68 | 6,684 must be sold by automation | $11,362.80 | $34,089.10 |
| Day 29 | $17,044.54 | $51,133.22 | 10,026 must be sold by automation | $17,044.20 | $51,133.30 |
| Day 30 | $25,566.81 | $76,700.02 | 15,040 must be sold by automation | $25,568 | $76,701.30 |
| Day 31 | $38,350.21 | $115,050.24 | 22,559 must be sold by automation | $38,350.30 | $115,051.60 |
| Day 32 | $57,525.32 | $172,575.55 | 33,838 must be sold by automation | $57,524.60 | $172,576.20 |
| Day 33 | $86,287.98 | $258,863.53 | 50,758 must be sold by automation | $86,288.60 | $258,864.80 |
| Day 34 | $129,431.96 | $388,295.49 | 76,136 must be sold by automation | $129,431.20 | $388,296 |
| Day 35 | $194,147.95 | $582,443.44 | 114,205 must be sold by automation | $194,148.50 | $582,444.50 |
| Day 36 | $291,221.92 | $873,665.36 | 171,307 must be sold by automation | $291,221.90 | $873,666.40 |
| Day 37 | $436,832.88 | $1,310,498.25 | 256,961 must be sold by automation | $436,833.70 | $1,310,500.10 |
Example problem using geometric series on how to become a millionaire in 37 days.
|
n2 =
is the second term or day 2, given information.
L2 =
is the money value at 2nd term or day two, given information.
a =
Answer, first term or first day initial money
|
n37th day =
L37th =
Value at 37th term or Day 37
compute the value at n12th = 12 value is 17.2995 at n24th = 24 value is 2,244.5483 at n48th = 48 value is 37,784,977.7905 at n50th = 50 value is 85,016,200.0285 n3rd day =
3 for 3rd day, given information. L3 =
L3 = 0.45 value of money on 3rd day, given information. r =
automatic computation of ratio.
|


The Graph of Geometric Function
y = a r n-1
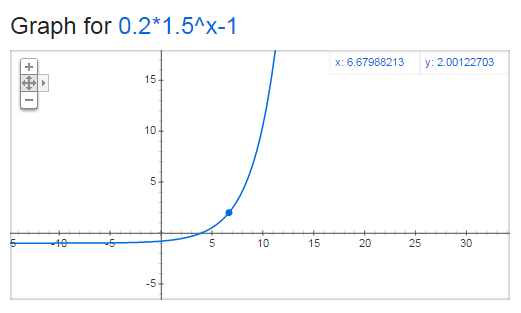
Notice the equation is similar to the Last Term equation Ln = a r n-1
Here a = first term of the series = 0.20 ;
r = geometric ratio = 1.5
And n = number of series is represented by the x-axis
While L = last term value is represented by the y-axis.
.
IN-V-BAT-AI helps you recall information on demand—even when daily worries block your memory. It organizes your knowledge to make retrieval and application easier.
Source: How People Learn II: Learners, Contexts, and Cultures
.
How can IN-V-BAT-AI be used in classrooms ?
IN-V-BAT-AI is a valuable classroom tool that enhances both teaching and learning experiences. Here are some ways it can be utilized:
⋆ Personalized Learning : By storing and retrieving knowledge in the cloud, students can access tailored resources and revisit
concepts they struggle with, ensuring a more individualized learning journey.
⋆ Memory Support : The tool helps students recall information even when stress or distractions hinder their memory, making it
easier to retain and apply knowledge during homework assignments or projects.
⋆ Bridging Learning Gaps : It addresses learning loss by providing consistent access to educational materials, ensuring that
students who miss lessons can catch up effectively.
⋆ Teacher Assistance : Educators can use the tool to provide targeted interventions to support learning.
⋆ Stress Reduction : By alleviating the pressure of memorization, students can focus on understanding and applying concepts,
fostering a deeper engagement with the material.
🧠 IN-V-BAT-AI vs. Traditional EdTech: Why "Never Forget" Changes Everything
📚 While most EdTech platforms focus on delivering content or automating classrooms, IN-V-BAT-AI solves a deeper problem: forgetting.
✨Unlike adaptive learning systems that personalize what you learn, IN-V-BAT-AI personalizes what you remember. With over 504 pieces of instantly retrievable knowledge, it's your cloud-based memory assistant—built for exam prep, lifelong learning, and stress-free recall.
- ✅ One-click access to formulas, calculators, and concepts
- 📧 No coding, no hosting—just email what you want to remember
- 📱 Live within 24 hours, optimized for mobile and voice search
- 💸 $30/year for 504 personalized knowledge sites (just 6¢ each)
"🧠 Forget less. Learn more. Remember on demand."
That's the IN-V-BAT-AI promise.
Personal Augmented Intelligence (AI) Explanation
🧠 Augmented Intelligence vs Artificial Intelligence
Understanding the difference between collaboration and automation

🔍 Messaging Contrast
Augmented Intelligence is like a co-pilot: it amplifies your strengths, helps you recall, analyze, and decide — but it never flies solo.
Artificial Intelligence is more like an autopilot: designed to take over the controls entirely, often without asking.
💡 Why It Matters for IN-V-BAT-AI
IN-V-BAT-AI is a textbook example of Augmented Intelligence. It empowers learners with one-click recall, traceable results, and emotionally resonant memory tools. Our “Never Forget” promise isn't about replacing human memory — it's about enhancing it.

Note: This is not real data — it is synthetic data generated using Co-Pilot to compare and contrast IN-V-BAT-AI with leading EdTech platforms.


.
.
.
🎉 50,000 Visitors Strong
IN-V-BAT-AI just crossed 50,000 organic visits—no ads, just curiosity and word-of-mouth.
Every visit is a step toward forgetting less, recalling faster, and remembering on demand.
Never Forget. Learn on demand.
SubscribeTry AI website hosting
$30 per year
| Year | Top 10 countries | Pages visited |
| 2023 | 1. USA 2. Great Britain 3. Germany 4. Canada 5. Iran 6. Netherlands 7. India 8. China 9. Australia 10. Philippines | 127,256 Pages / 27,541 Visitors |
| 2024 | 1. USA 2. China 3. Canada 4. Poland 5. India 6. Philippines 7. Great Britain 8. Australia 9. Indonesia 10. Russia | 164,130 Pages / 40,724 Visitors |
| Daily Site Visitor Ranking 10/10/2025 | 1. USA 2. Brazil 3. Vietnam 4. Canada 5. India 6. Argentina 7. Morocco 8. Japan 9. Indonesia 10. Ecuador | Year to Date 166,990 Pages / 55,839 Visitors |
Data source: Advanced Web Statistics 7.8

























